Introducción
Todos los días nos enfrentamos a “fenómenos irreversibles” y espontáneos que, a simple vista, no parecerían ameritar un interés mayor al cotidiano; pero si nos detuviéramos a pensar en ellos con un pequeño conocimiento de física, muy probablemente muchas interrogantes surgirían.
Así, hechos simples como, por ejemplo, una hoja de papel quemada no puede regresar a su estado inicial; del mismo modo, tampoco, a medida que envejecemos, podemos rebobinar nuestros relojes internos y recuperar nuestra juventud.
Podríamos tal vez preguntarnos, en este punto, la razón tras estos sucesos de la vida diaria y pensar en esa famosa y aludida “flecha del tiempo” que indica la dirección clara hacia la cual se mueven los eventos de manera consistente.
Como se entiende actualmente, todo obedece a las leyes de la física. La Segunda Ley de la Termodinámica establece que los sistemas progresan naturalmente del orden al desorden (lo que se conoce como entropía, una tendencia presente en todo el universo) y que, en todo proceso espontáneo, la entropía total del sistema y de su entorno aumenta. Los sistemas vivos, aunque localmente mantienen el orden, contribuyen al aumento global de esta, como veremos más adelante [1].
Sin embargo, es importante aclarar que actualmente el término “entropía” tiene varias connotaciones. Si lo hemos escuchado anteriormente, puede ser que estemos más familiarizados con una definición de entropía que proviene de las clases de biología y química que se nos impartieron durante nuestra formación académica, y en las que se definía la entropía como esa tendencia del universo al desorden que ya hemos mencionado anteriormente.
Esta entropía, en su connotación termodinámica, se considera que está en todas partes (desde los agujeros negros, la evolución y hasta el envejecimiento) y siempre tiende a aumentar. A medida que el desorden del sistema aumenta, el número de estados disponibles del sistema aumenta y la energía está menos concentrada [2]. Podríamos preguntarnos, llegados a este punto, ¿qué sucede con los organismos vivos?
A partir de la fecundación, el organismo humano se constituye como un sistema abierto que, mediante procesos biológicos coordinados, alcanza una organización multicelular compleja y funcional, manteniendo su estabilidad interna pese al aumento continuo de la entropía propia de los procesos biológicos. El mundo vivo se caracteriza por una complejidad y, paradójicamente, un orden creciente [3, 4].
¿Es la vida en sí una excepción a la regla?, ¿un desafío al orden natural?
Y, en efecto, vivimos en un universo en el que, a pesar de que existe una creciente entropía, está repleto de estructuras ordenadas como estrellas, planetas e incluso nosotros mismos. Pero ¿por qué ocurre esto? Comprenderlo significa entender la vida misma desde su origen, lo que es esencial para actuar en ella e intentar mantenerla.
Para que los sistemas biológicos puedan funcionar deben permanecer alejados del equilibrio. Este “equilibrio” se refiere a la homogeneidad de todos los elementos que forman parte de un sistema, sin que existan gradientes ni diferencias dentro de él y con el medio externo. Esta valiosa observación llevó al desarrollo de “la termodinámica del no equilibrio”, que establece que, si se produce una reacción espontánea, esta tiende hacia un estado de equilibrio termodinámico y, en ese proceso, se vuelve cada vez más aleatoria o desordenada. Es este creciente desorden o entropía del sistema lo que hace que la reacción espontánea persista; pero, una vez que el sistema alcanza la entropía máxima o el equilibrio, la reacción espontánea deja de continuar: no hay gradiente de energía y se detienen todos los procesos, incluidos los biológicos, lo que para los sistemas vivos es equivalente al fin de la vida [1, 3].
Como exploraremos en las siguientes secciones, muchas de las afirmaciones que intentan explicar estos fenómenos aún son consideradas teorías o interpretaciones científicas en busca de la respuesta a una de las preguntas más inquietantes e importantes que se han hecho: ¿cómo surgió la vida?
Entropía: una palabra con un mar de interpretaciones
El término entropía, como hemos comentado, puede tener múltiples definiciones operacionales. En este sentido, el término entropía en su conceptualización termodinámica clásica (como la magnitud física medible del desorden de un sistema) es un hilo conductor muy útil que seguiremos utilizando a lo largo de esta revisión [7].
Sin embargo, entre las distintas definiciones de entropía existe una que resulta particularmente útil al tratar de entender los sistemas biológicos. El físico teórico y matemático Ludwig Boltzmann definió a la entropía como aquella medida de la cantidad de microestados posibles de un sistema que producen el mismo macroestado [1]. Si la cantidad de microestados posibles es alta para el macroestado, se dice que la entropía es alta (el sistema está altamente desordenado); en cambio, si la cantidad de microestados posibles es baja, se dice que la entropía es baja (el sistema está altamente ordenado) [5]. Esta interpretación implica principalmente un concepto de posibilidades. Por tanto, cuanto mayor sea el número de microestados compatibles con un mismo macroestado, mayor será la entropía y menor será el grado de orden macroscópico [1, 6].
Cabe resaltar, como se mencionará en secciones posteriores, que la entropía va más allá de su conceptualización termodinámica como “desorden” o de la distribución de posibilidades; por ejemplo, la entropía informacional corresponde a la cantidad de información contenida o transmitida por una fuente de información [7]. Esto no contradice ni se superpone a la entropía en su conceptualización termodinámica ni a la definición de Boltzmann, sino que ofrece otra “lente” para mirar el mismo fenómeno. Es decir, la entropía tiene diversos matices o planos dependiendo del contexto en el que se vea, complementándose una interpretación con otra, de allí su complejidad y, a su vez, su belleza.
Entropía y evolución
La entropía y la evolución, como indica el físico Brian Greene, son aquella extraña y a la vez extraordinaria pareja en este camino hacia el entendimiento del origen de la vida. Se cree en teorías recientes que la vida en la Tierra se desarrolló bajo una presión evolutiva, operando también a nivel molecular; esto es conocido como el “darwinismo molecular”, este combate químico en la lucha por la supervivencia en el que se produjeron una serie de mutaciones y configuraciones que finalmente llevaron a la primera colección de células que se reconocieron como vida [8, 9].
Por tanto, la selección darwiniana se considera un punto crucial en la transición de la materia inerte a la materia viva.
La materia viva evade la degradación al equilibrio
El físico Erwin Schrödinger mencionó en su afamado texto “¿Qué es la vida?” de 1944 que lo que diferencia a un sistema vivo de uno no vivo es su capacidad de continuar realizando actividades, moviéndose e intercambiando materia con su entorno durante un período mucho más prolongado del esperado, y manteniéndose lejos del equilibrio termodinámico [10, 11].
Cuando esto no ocurre, el sistema se desvanece en una masa de materia inerte. Schrödinger lo llamó “estado de equilibrio termodinámico” o “de entropía máxima”, en donde todas las partes de un sistema alcanzan el equilibrio térmico a una temperatura uniforme. Después de ese punto no serían posibles más cambios que impliquen la liberación de calor y de transformaciones que generen trabajo útil [10]. Toda la energía se distribuiría uniformemente, impidiendo cualquier otro proceso físico o vida.
Es al evitar la rápida descomposición a este estado inerte de “equilibrio” que un organismo parece volverse único. Tan fascinante como aquella observación es la pregunta: ¿cómo evita el organismo vivo dicha descomposición? La respuesta es: comiendo, bebiendo, respirando y, en el caso de las plantas, asimilando. Es decir, llevando a cabo lo que se conoce como metabolismo o, en otras palabras, intercambio y transformación de materia y energía [3, 10].
Un sistema aislado no intercambia materia ni energía con su entorno, mientras que un sistema abierto intercambia ambas [12].
Los organismos vivos no están aislados, son considerados sistemas abiertos [13, 14] y, por lo tanto, la Segunda Ley de la Termodinámica se aplica tanto a los sistemas vivos como al entorno donde se encuentran, lo cual se denomina “los dos pasos entrópicos”, concepto introducido por el físico Brian Greene [15]:
• En el primer paso, se produce una disminución localizada de la entropía cuando se forman estructuras ordenadas dentro del sistema vivo utilizando energía (el sistema vivo absorbe energía del ambiente para ordenarse) [15].
• En el segundo paso, se produce un mayor incremento de la entropía en otras partes del universo, mediante la liberación de calor residual al ambiente [15].
Todo proceso, evento o acontecimiento implica un aumento de la entropía. Así, un organismo vivo aumenta continuamente la entropía del universo: produce y exporta “entropía positiva” (calor), mientras dentro de él mantiene el orden [16].
Schrödinger introduce el concepto de “entropía negativa” (abreviada neguentropía) como la base de la organización biológica, planteando que los seres vivos se “alimentan” de orden (luz solar) para mantener su estructura lejos del equilibrio [10, 14]. En este contexto, la neguentropía describe procesos locales de organización que ocurren dentro del marco general impuesto por la Segunda Ley de la Termodinámica [7].
En un organismo, el grado de desorganización interna es la entropía y el grado de organización interna es la neguentropía. En otras palabras, en un sentido metafórico, la neguentropía se utiliza sistemáticamente como sinónimo de fuerza de cohesión, mientras que la entropía es sinónimo de fuerza de repulsión [7, 17].
La vida, por tanto, se mueve dentro de las Leyes de la Termodinámica. Lo esencial en el metabolismo es que el organismo logre (o intente hacerlo) librarse de la mayor cantidad de entropía que inevitablemente produce mientras vive, para evitar su muerte [14].
Ejemplificaciones biológicas sobre la entropía
El punto anterior muy bien lo resumió el químico Albert Lehninger así:
“El orden que se produce dentro de las células a medida que crecen y se dividen se ve más que compensado por el desorden que crean en su entorno. La vida preserva su orden interno al tomar energía gratuita del entorno y devolver una cantidad igual o mayor en forma de calor y entropía” [18].
Para que estos conceptos, algo abstractos, se entiendan un poco mejor, utilizaré unos sencillos ejemplos a continuación.
La fuente última de toda nuestra energía y entropía negativa es la radiación solar. La Tierra, por tanto, se considera un sistema cerrado al intercambio de materia y abierto al intercambio de radiación con el espacio. Este intercambio de radiación con el espacio impulsa y mantiene casi todos los procesos dentro de la Tierra [3, 19].
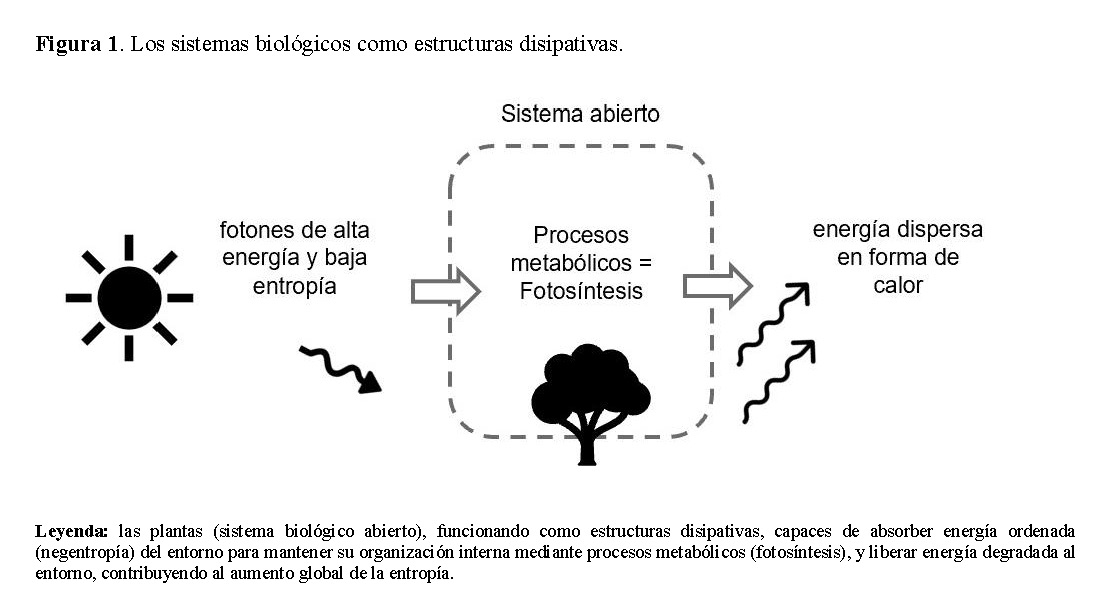
Las plantas también son un claro ejemplo de este principio. Los fotones (energía con baja entropía y, por tanto, ordenada) son absorbidos por las plantas, y la maquinaria celular los utiliza para mantener sus funciones celulares. Por cada fotón recibido del Sol, la Tierra envía una colección mucho menos ordenada de fotones depletados de energía y ampliamente dispersos de vuelta al espacio [15, 18].
Organismos vivos como estructuras disipativas
Para el físico y químico Ilya Prigogine, la evolución tenía que haber sido reconceptualizada como el estudio del surgimiento, cambio, propagación y adaptación de redes de “estructuras disipativas autorreplicantes” [20]. En termodinámica, una estructura disipativa es una estructura que surge espontáneamente en sistemas alejados del equilibrio, se mantiene consumiendo energía libre y aumentando eficientemente la entropía en su entorno [12, 21].
La Segunda Ley de la Termodinámica postula que todas las acciones incrementan el desorden del sistema en el que se producen y consumen energía utilizable al hacerlo [22]. Podemos considerar, por lo anterior, que la vida emergió como consecuencia de procesos físicos que favorecieron estructuras capaces de disipar energía.
Los sistemas biológicos son estructuras disipativas autoorganizadas. Absorben energía del entorno para mantener los procesos vitales y luego liberan calor al entorno y, al hacerlo, funcionan en un estado de no equilibrio [21].
Para comprender mejor la vida, entonces, se requiere una perspectiva termodinámica que entienda a los organismos vivos como estructuras que emergen de la disipación de energía libre en sistemas complejos, que evolucionan mediante selección natural para reproducir su estructura, utilizar y degradar la energía libre con mayor eficacia (Figura 1) [22].
Procesos: energía e información
Los procesos y condiciones que ocurrieron en el pasado han dado lugar a aquello en lo que se han convertido los organismos vivos hoy en día. Los organismos vivos son sistemas que evolucionan porque han sido “informados” por los entornos en los que viven. Su forma y organización no surgieron de la nada, sino como resultado de eventos irreversibles (mutaciones y selección natural) que dejaron huellas permanentes [9, 23].
Estos procesos pueden englobarse en tres bien definidos puntos:
El primer proceso es el mantenimiento y la producción de masa biológica mediante el uso de la energía y la materia disponibles. Sin un flujo continuo de energía, se perderá la separación de fases con el entorno, con el riesgo de alcanzar el equilibrio térmico [23, 24].
• Las transformaciones que generan calor producen “entropía térmica”: una medida del costo de mantener la estructura biológica [25].
• Las transformaciones conservativas producen “entropía estructural”: una medida de la complejidad estructural del sistema [25].
En segundo lugar, los sistemas biológicos mantienen su integridad estructural y funcional mediante el almacenamiento y la transmisión de información. Sin la acumulación y expresión de información, los sistemas biológicos no podrían retener patrones exitosos de flujo de energía que mejoraran su capacidad para mantener el orden [23].
La información genética es un tipo particular de información. En el ácido desoxirribonucleico (ADN), los nucleótidos forman arreglos con propiedades tanto entrópicas como representacionales, que generan niveles de integración jerárquicos: tripletes → aminoácidos → proteínas → funciones reguladoras, donde cada nivel impone restricciones sobre los inferiores [24, 26].
La entropía informacional de un sistema depende del número de configuraciones posibles que puede adoptar la información inicial. Así, un macroestado informacional (como un gen funcional) puede expresarse mediante muchos microestados posibles (variantes de secuencia), y su entropía refleja estas probabilidades [24].
Como indicó Prigogine, los seres vivos son sistemas autocatalíticos informados, por lo que las “reglas de producción internas” que determinan gran parte de las formas biológicas sobre las que opera la selección están determinadas por la información transmitida al sistema desde sistemas ancestrales [26].
Finalmente, como consecuencia del flujo de energía, se producen diferentes tipos de entropía a diferentes ritmos [23]. No existe un único nivel organizacional, sino diversos niveles, y cada uno de ellos interactúa con los demás de diversas formas:
• En niveles microscópicos (celulares) domina el metabolismo: la entropía se disipa como calor metabólico, y los organismos se comportan como estructuras disipativas clásicas [24].
• En escalas más amplias y duraderas (procesos genéticos y evolutivos), la entropía está vinculada a la diversidad genética [24].
La información genética puede considerarse, en este sentido, una forma de entropía organizada: un registro estable del flujo energético que dio origen a la vida, enlazando así los principios termodinámicos con la evolución molecular [27].
De la física a la biología molecular
La materia viva, especulaba Schrödinger, se regía por “un cristal o sólido aperiódico”, quien para mediados de los años cuarenta expresó la siguiente hipótesis: “Creemos que un gen o quizás toda la fibra cromosómica es un ‘sólido aperiódico’” [10].
Este tipo de estructura molecular no repetitiva que albergaba “el código cifrado de la herencia” daría lugar al “patrón completo del desarrollo futuro del individuo y de su funcionamiento en la madurez”, dando así una descripción temprana del ADN [2].
Schrödinger, por tanto, dedujo en aquel entonces, como bien reafirma el físico Sean Carroll, que la estabilidad de la información genética en el tiempo es mejor explicada por la existencia de ese cristal aperiódico que guardaba información en su estructura química [28]. Esto permitió e inspiró a Francis Crick a abandonar la física a favor de la biología molecular, eventualmente llevándolo a su descubrimiento con James Watson de la estructura de la doble hélice del ADN [2].
En palabras de Watson:
“Desde el momento en que leí ¿Qué es la vida? de Schrödinger concentré todos mis esfuerzos en encontrar los secretos del gen” [2].
Organización a nivel celular
Los organismos vivos son entidades complejas, ordenadas e improbables. Estos tienen una entropía extraordinariamente baja porque la selección natural les otorgó adaptaciones que, en última instancia, permitieron la replicación genética [6].
Cada célula diploide alberga dos copias de cada cromosoma. Estas células, dispersas por todo el cuerpo, están comunicándose entre sí con gran facilidad gracias al código genético. Su desarrollo regular y ordenado se rige por este principio rector en cada célula, que puede dar lugar a eventos que son paradigmas de orden [3, 29].
Según lo estipulado por Schrödinger, existen dos mecanismos diferentes mediante los cuales se llega a este orden: el mecanismo que produce orden a partir del desorden (metabolismo) y aquel que produce orden a partir del orden (replicación) [2, 30].
La replicación es un proceso complejo y requiere organismos complejos y altamente ordenados. Si el organismo tiene éxito para sobrevivir y reproducirse, los genes que codifican estas adaptaciones son capaces de replicarse. Estos genes, por tanto, pueden identificarse como los replicadores en este proceso y el organismo como su medio de selección [6, 31].
El mecanismo, por otro lado, de orden a partir del desorden (ya explicado previamente) es el que más se presenta en la naturaleza y permite comprender la gran línea de los eventos naturales, como su irreversibilidad.
ADN
Si la entropía está en todo el universo, ¿existe entropía en el ADN? La respuesta es sí, pero no en su conceptualización termodinámica de desorden, sino como medida de información (complejidad, variabilidad o predictibilidad). ¿Qué implica esto?
Hasta este punto, la entropía ha sido abordada como una magnitud física asociada a energía y microestados. Sin embargo, cuando el objeto de estudio es el ADN, la entropía adquiere un matiz distinto: no describe flujos energéticos, sino que se emplea, en cambio, como una medida del contenido de información y de la complejidad de la secuencia [32].
La mayoría de los sistemas biológicos (incluido el genoma humano) contienen información en forma de ADN. Es sobre estos sistemas físicos que almacenan y procesan información que opera la Segunda Ley de la Termodinámica para generar complejidad, variedad y orden biológico.
En estos sistemas, las secuencias de ADN de gran tamaño y de estructura compleja contienen regiones que han acumulado un alto contenido de “ADN errático” durante la evolución; el ADN, en este contexto, puede verse como una estructura fuera de equilibrio [32]. Aunque compleja, la información biológica puede expresarse en términos de un fenómeno entrópico: cuanta más información contiene un sistema, mayor es la entropía que posee en el marco informacional [7, 32].
La falta de consenso sobre el significado biológico de la entropía y la complejidad de los genomas, así como las diferentes formas de evaluar estos datos, dificultan la obtención de conclusiones sobre las causas de la variación de la entropía genómica entre especies [33].
La entropía informacional, como medida del contenido y la complejidad de la información, fue introducida por primera vez por el matemático Claude Shannon en 1948. Desde entonces, ha adoptado diversas formas y metodologías para su análisis [32, 34, 35].
La entropía de Shannon cuantifica la imprevisibilidad estadística de los elementos (como nucleótidos) en una secuencia: un mensaje con alta predictibilidad tiene menor contenido de información que un mensaje menos predecible [36, 37], mientras que, por otro lado, la entropía topológica evalúa la complejidad estructural y las variaciones locales, proporcionando una caracterización aproximada de la aleatoriedad. Así, una entropía topológica baja en una secuencia implica que esta es menos caótica y más estructurada [32].
En esta línea, Vopson propuso el principio de equivalencia “masa-energía-información”. En pocas palabras, los sistemas evolucionan hacia estados de menor entropía informativa al reducir la aleatoriedad, aumentando así su capacidad de almacenamiento y control de la información [27].
En el genoma humano, se estima que el 5 % del ADN está bajo presión de selección, pero solo el 1,5 % de este ADN se considera codificante. Esto implica que los elementos del ADN no codificante están también bajo presión de selección y, por consiguiente, desempeñan funciones significativas [38].
¿Dónde hay mayor entropía, entonces?
Los resultados son contradictorios. Algunos estudios han estimado que el ADN no codificante tiene una entropía menor que el ADN codificante, mientras que tres estudios (Mazaheri et al., Koslicki y Jin et al.), utilizando la entropía topológica, concluyeron que el ADN no codificante tiene una entropía mayor que la del ADN codificante [38]:
Estudios recientes aplicando definiciones de entropía topológica a muestras aleatorias sistemáticas de genes de todos los cromosomas del genoma humano han concluido que los intrones tienen una entropía mayor que los exones [32]. ¿Qué podría explicar este resultado?
Se sabe que la entropía mide la aleatoriedad de una secuencia de ADN, y se espera que los intrones se comporten de forma más aleatoria, ya que presentan menor presión selectiva, tienen menos señales funcionales y, por tanto, están menos conservados que los exones [32].
La entropía del cromosoma X, tanto en intrones como en exones, es significativamente mayor que la del cromosoma Y [32].
En el estudio de Koslicki, la media de las entropías de los intrones del cromosoma X fue de 3,5 desviaciones estándar mayor que la media de las entropías de los intrones del cromosoma Y. En este estudio también se observó que los intrones del cromosoma Y presentaron una entropía atípicamente baja y bimodal, que posiblemente corresponda a secuencias aleatorias (intrones con alta entropía: mayor que 0,910) y secuencias intrónicas con estructura o función oculta (baja entropía: menor a 0,910) [32].
¿Qué hay de otras regiones en el genoma humano?
Siepel et al. demostraron que tanto las regiones UTR 5' como las 3' se encuentran entre los elementos más conservados en los genomas de vertebrados. Por lo tanto, la entropía topológica, es decir, el grado de las variaciones en la secuencia de estas regiones, es muy baja, lo que indica un alto grado de estructuración [38].
La entropía del ADN está influenciada por las bases nitrogenadas.
En diversos estudios, los perfiles de entropía creados para 16 genomas procariotas revelaron diferencias en la complejidad entre genomas ricos en citosina-guanina (CG) y adenina-timina (AT). En ellos, todos los perfiles porcentuales de CG mostraron los mayores aumentos cuando incluyeron ADN codificante, conocido por ser más rico en CG que el ADN no codificante [4].
Todo esto respalda la afirmación de que la entropía topológica puede utilizarse para detectar regiones funcionales y regiones sometidas a restricción selectiva [24]. Por tanto, la genética, aunque inicialmente no parezca tan asociada a la entropía como otras ciencias, juega un rol preponderante en su entendimiento.
El ser humano como un sistema biológico
En evolución, aunque aún debatible, existe la idea de que poblaciones pequeñas podrían acumular duplicaciones o elementos repetitivos que aumentan su tamaño genómico, pero presentando “menor entropía informacional” porque se encuentra restringido el número de microestados válidos para un macroestado funcional. Es decir, se trataría así de genomas de gran tamaño, pero con alta redundancia [39].
En este sentido, pareciera existir una aparente falta de correspondencia directa entre el aumento del tamaño, la complejidad estructural del genoma y los valores de entropía medidos. Esta discrepancia no refleja una contradicción real, sino que surge de emplear definiciones distintas de entropía para describir un fenómeno.
Estas distinciones conceptuales permiten comprender por qué una región del ADN puede exhibir alta entropía desde el punto de vista informacional (indicando secuencias altamente variables o impredecibles) sin que ello implique un mayor desorden funcional u organizacional. De esta misma forma, regiones funcionales y evolutivamente conservadas muestran baja entropía informacional, no por simplicidad estructural, sino porque la selección natural restringe severamente el conjunto de secuencias viables. En este marco, la entropía deja de ser una noción abstracta de “desorden” para convertirse en una medida de la “diversidad” de configuraciones funcionales accesibles al sistema biológico [4, 24, 32].
Por tanto, hablar de entropía y su relación con el ADN amerita una explicación rigurosa de la definición usada: termodinámica, de Boltzmann o informacional; una vez delimitado este marco, las aparentes contradicciones desaparecen y las distintas medidas se vuelven herramientas complementarias para determinar función, conservación, complejidad y patrones de organización en el genoma.
En términos biológicos, el ser humano es una maquinaria extraordinaria de cientos de sistemas dentro de él, cada uno destinado a jugar un rol vital para que este sistema biológico funcione y sobreviva. Por ello, la desviación del orden de tan solo unos pocos átomos dentro del grupo de átomos reguladores de la célula germinal basta para producir un cambio bien definido en las características hereditarias a gran escala del organismo.
De un orden potencial que somos capaces de alcanzar, asimismo somos susceptibles a experimentar alteraciones en estos procesos, que pueden producir una desorganización estructural, volviéndonos proclives a procesos adversos (malformaciones, disrupciones, crecimiento incontrolado) y, dependiendo de su severidad, pueden llevarnos a la muerte [40].
Cuando el orden celular se pierde, la entropía aumenta. Esto se traduce en una proliferación, en muchas ocasiones acelerada y desorganizada. Un simple cambio en el orden usual sobreviene a un aumento de la entropía y a consecuencias adversas.
Las células cancerígenas son un claro ejemplo de esta afirmación.
El cáncer y la entropía
Una transición fundamental en la evolución de la vida ha sido el paso de los organismos unicelulares a los pluricelulares. En esta etapa, cada célula tuvo que transferir sus principales cualidades (sobrevivir y multiplicarse) al organismo [39].
Algunas de estas células cancerosas evolucionarán hacia un estadio invasivo y metastásico. Por tanto, algunos autores clasifican al cáncer como una degradación de los sistemas biológicos de información y comunicación [40].
¿Cuál es el rol de la entropía, por tanto, en el cáncer?
El concepto de entropía (sea estructural, genómica, transcriptómica o de transducción de señales) se ha aplicado repetidamente a las características del tejido o de las células cancerosas. De ellas, el aumento de la entropía de señalización se ha estudiado ampliamente como una característica del cáncer [41].
Aquí solo ilustraré tres puntos, a mi parecer, de relevancia para entender un poco mejor esta relación.
La génesis del cáncer y su relación con la entropía es sumamente compleja.
La entropía de señalización puede, en una célula, favorecer la aparición de eventos oncogénicos, por ejemplo, con la pérdida del control negativo sobre la proliferación celular. Otros cambios positivos en estas células aumentarán aún más la competitividad y, así, la célula tumoral habrá acumulado suficientes ventajas como para volverse independiente de la regulación fisiológica normal [39].
Igualmente, la diversidad de combinaciones de mutaciones encontradas entre los distintos tipos de cáncer es consecuencia de un mecanismo impulsado por la entropía, como la activación de un protooncogén o la inactivación de un gen supresor tumoral, combinada con mutaciones específicas de cada cáncer (pasajeras o facilitadoras) [39].
Resumiendo, la carga colectiva de perturbaciones en las células cancerosas tiene un efecto desestabilizador en la red reguladora de genes, aumentando la entropía de señalización. Este aumento de la entropía produce que las células cancerosas sean más propensas a la transición entre estados celulares e incluso tipos celulares [41].
Pero la relación con la entropía no se detiene allí.
La aneuploidía resultante de una mitosis defectuosa es una causa común de aumento de la entropía de señalización en el cáncer, generando un aumento en la proliferación celular [39].
Los microARN (miARN) son reguladores precisos de la biología celular; por tanto, pueden considerarse guardianes ideales contra el aumento de la entropía. El papel de la regulación negativa de los miARN en el cáncer ha sido ampliamente estudiado. En distintos tipos de tumores se ha documentado una disminución global de los niveles de miARN, así como defectos en diversas etapas de su síntesis, principalmente por silenciamiento epigenético [39].
Resistencia al tratamiento oncológico
Se ha evidenciado que se produce un aumento acelerado de la entropía en las células cancerosas impuesto por la terapia contra el cáncer, lo que permite a las células cancerosas explorar una región más amplia del espacio de “fases de expresión génica”, otorgándoles la oportunidad de alcanzar “atractores” (estadios de energía mínima) normalmente latentes, correspondientes a fenotipos más agresivos. Esto, finalmente, favorece la aparición de nuevas mutaciones y produce resistencia a las terapias dirigidas a mutaciones oncogénicas existentes [42].
Esto se ha evidenciado, por ejemplo, en el tratamiento de melanomas y, de manera similar, en el cáncer de mama, donde se han identificado células cancerosas quiescentes preexistentes resistentes a los inhibidores de tirosina-quinasa contra HER2 (receptor 2 del factor de crecimiento epidérmico humano) [39, 42].
Envejecimiento y muerte
La vida, por todo lo que se ha podido retratar a lo largo de este trabajo, no rechaza la entropía, sino que experimenta y vive con ella hasta entrar en un colapso final inevitable. Pero justo antes de este colapso encontramos una situación más donde la entropía juega un rol preponderante en su génesis.
La entropía y el envejecimiento están estrechamente relacionados: el envejecimiento puede interpretarse como una consecuencia del aumento de la entropía. La integridad de la red génica disminuye con la edad, como se ha observado en modelos animales, donde el análisis de decenas de conjuntos de datos de expresión génica tisular en ratones y humanos envejecidos demuestra una sobreexpresión de inflamación, apoptosis y senescencia [39].
Como se ha revisado extensamente, la entropía en los sistemas siempre tiende a aumentar. Se ha evidenciado que la entropía de Shannon tiende a aumentar con la edad, al igual que los sitios CpG (regiones en el ADN donde hay citosina seguida de guanina) en los “relojes epigenéticos de Horvath” (marcadores de edad biológica), mostrando más entropía, es decir, más variabilidad en la metilación [31]. De esta forma, se establece la relación entre la entropía y el envejecimiento.
Pero no es la única relación. Desde una perspectiva termodinámica, el ser humano es una estructura disipativa lejos del equilibrio, pero con el envejecimiento este sistema se vuelve progresivamente ineficaz para intercambiar y distribuir energía, incluida la transferencia de la entropía negativa del ambiente al organismo, volviéndolo proclive a la aparición de enfermedades y a la muerte [31].
El ser humano, con el tiempo, pierde así su capacidad para disipar y contrarrestar el creciente flujo de entropía positiva (ese desorden acumulado a lo largo del tiempo), aproximándose eventualmente a aquel equilibrio térmico donde el flujo de energía cesa y el sistema colapsa.
Conclusiones
La vida puede entenderse como un proceso natural compatible con la Segunda Ley de la Termodinámica, permitiéndole a los sistemas biológicos mantener un alto grado de orden local a costa de incrementar la producción de entropía en su entorno, actuando así como sistemas abiertos y disipativos.
Este enfoque propone una lectura de la vida como una de las múltiples maneras en las que estas leyes pueden manifestarse en sistemas alejados del equilibrio. Así, la vida mantiene su estructura interna no al margen de la entropía, sino dentro de sus límites, utilizándola como un medio de estabilidad dinámica.
Como se ha expuesto previamente, la entropía enmarca y condiciona los procesos biológicos: desde nuestra concepción, desarrollo, crecimiento y hasta el envejecimiento; y, desde el quehacer médico, se manifiesta como un eje silencioso que subyace a los mecanismos biológicos que, como clínicos, observamos, estudiamos y abordamos en cada paciente, tanto en procesos fisiológicos como patológicos.
Está implicada en procesos macroscópicos y microscópicos, incluso en eventos adversos como el cáncer, pero también guarda una increíble relación con los procesos evolutivos que nos han llevado a lo que somos hoy en día. Es imposible hablar de la supervivencia humana sin que la vida haya enfrentado y prevalido (aunque no derrotado) a la inmensurable entropía que nos rodea día con día.
Resta determinar si esa cadencia dual determinada por la entropía podrá sostenerse en escalas cosmológicas o si, a largo plazo, el universo evolucionará a ese estado de máxima entropía donde no hay gradiente energético y sobrevendrá la denominada “muerte térmica” del universo.
Quiero finalizar esta pequeña disertación con las palabras del físico teórico y uno de los principales exponentes de la “teoría de las cuerdas”, Brian Greene:
“Todos, de una u otra forma, tratamos de darle sentido al mundo que nos rodea. Y todos estos elementos se encuentran en el núcleo de la física moderna. La historia es de las más grandiosas: la expansión de todo el universo; el misterio es de los más difíciles: descubrir cómo surgió el cosmos… y la búsqueda es de las más profundas: la búsqueda de leyes fundamentales que expliquen todo lo que vemos y lo que está más allá, desde las partículas más diminutas hasta las galaxias más lejanas” [43].
Agradecimientos
Gracias al Dr. Enrique Daniel Austin-Ward MD, Genetista, Centro Nacional Especializado de Genética Médica y Genómica, Caja de Seguro Social, Panamá; por sus contribuciones.
